一定速度で発射した物体が描く放物線の包絡線

経緯

前にこんなツイートを見かけました。

筑駒の野球部の顧問の先生は筑駒名物の物理の先生で、高１の期末試験の最後の問題は「バッターが打った時の最大のボールのスピードをa km/hとしたときに、絶対にボールが当たらない最小のドームの天井部分の式を作れ。」だった（条件設定は当時の記憶が曖昧なのでちょっと違ったかも）。楽しかった。 https://t.co/Lan8WRxHUd
— Hirofumi Seo (@HirofumiSeo) 2018年8月26日

実はこれ、京大の過去問にあります（'00後期）。

最大の初速度 $v_0$ で、あらゆる方向に打ち分けることができる最強の打者を考慮して、ドーム球場（屋根付き野球場）を設計したい。座標の原点Oをホームベース上にとり、ボールが飛ぶ鉛直面内で原点Oから水平方向に $x$ 軸を、また鉛直上向きに $y$ 軸をとる。ただし、簡単のため、ボールは原点Oで打たれるものとする。また、重力加速度の大きさを $g$ とし、空気抵抗およびボールの大きさは無視できるものとする。
初速度 $v_0$ で打たれたボールが、打ち上げ角度に拘わらずドームの天井に当たらないためには、ホームベースから $R$ だけ離れた地点での天井の高さはいくつより大きくなければならないか。

要するに、以下の図で $\theta$ が変化するときボールが通過しうる領域はどこかという問題です。
f:id:nexusuica:20181111230158p:plain:w400

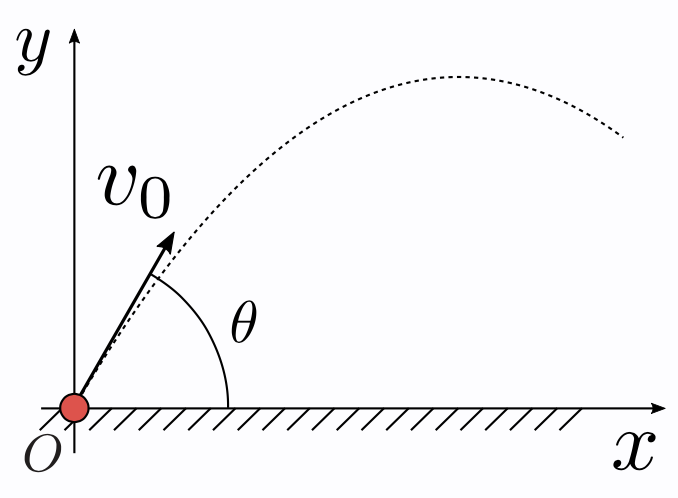
（図：https://physnotes.jp/exercises/shahou_orb/）

まずやることは適当な角度 $\theta$ での物体の軌跡を求めることです。これは、時刻 $t$ における物体の位置
　 $\displaystyle x=v_0t\cos\theta,\ y=v_0t\sin\theta-\frac12gt^2$
から $t$ を消去して、
　 $\displaystyle y=x\tan\theta-\frac{gx^2}{2v_0^2\cos^2\theta},\ y\geq0$
となります。あとはこれを $0<\theta<\frac{\pi}2$ で変化させたときにこの放物線が通過する領域を求めればよいわけです。通過領域を求めるには

順像法
逆像法
包絡線の計算

の3つのやり方があり、どれでもできます。とりあえず $\theta$ が複雑で鬱陶しいので $a=\tan\theta$ とおいておけば
　 $\displaystyle y=ax-\frac{(1+a^2)gx^2}{2v_0^2}$
となります。

順像法

順像法とは、「ある直線上のみでの通過範囲を求める」ことによって通過領域を求める方法です。今回であれば「ある $x$ 座標のみを考えたときに、 $\theta$ を変化させたとしてどこを通過するか？」を考えます。つまり、 $x$ を固定して $y$ を $\theta$ の関数と見てその値域を求めることになります。
いま、 $y$ は $a=\tan\theta$ の2次関数なのでその値域は平方完成することによって容易に求まり、
　 $\displaystyle y=-\frac{gx^2}{2v_0^2}\left(a-\frac{v_0^2}{gx}\right)^2+\frac{v_0^4-g^2x^2}{2gv_0^2}$
より、 $y$ の値域は
　 $\displaystyle 0\leq y\leq \frac{v_0^4-g^2x^2}{2gv_0^2}$
となります。結局これは鉛直投げ上げ運動の最高到達点 $\displaystyle \frac{v_0^2}{2g}$ を頂点とする放物線になっています。
www.desmos.com

逆像法

今度は逆像法です。逆像法とは、「ある点 $(x,y)$ を曲線が通過するようなパラメータの値が存在するかどうか」という存在条件から通過領域を求める方法です。今回は軌跡の方程式をパラメータ $a$ の方程式とみて $a$ の存在条件を求めます。方程式を $a$ について整理すると
　 $gx^2a^2-2v_0xa+2v_0^2y+gx^2=0$
となります。いま $a$ の取りうる範囲は $a>0$ なので、この範囲に解を少なくとも1つもつ $(x,y)$ の条件を求めればよいことになります。左辺は $a$ の2次関数になっていて、その放物線の軸は $x>0$ のもとでは $a>0$ に存在します。また、左辺を $f(a)$ とおくとき
　 $f(0)=2v_0^2y+gx^2>0$
より、 $a\leq 0$ には実数解は存在しえないことがわかり、結局たんに実数解をもつ条件のみを求めればよいです。これは判別式を使って、
　 $\displaystyle (v_0x)^2-gx^2(2v_0^2y+gx^2)\geq 0\Leftrightarrow y\leq \frac{v_0^4-g^2x^2}{2gv_0^2}$
と、同じ結果が得られます。

包絡線を直接求める

これまでは関数の値域や文字の存在条件から曲線の通過領域を求めましたが、この通過領域の境目には、もとの放物線が接しながら動きます（先ほどのグラフを参照）。このようにある曲線のパラメータを変化させたときにその曲線が常に接しながら動く曲線のことを包絡線といい、これを直接求める方法が存在します。
詳しいことはここに書いてあります。
mathtrain.jp
ここでは曲線を
　 $\displaystyle f(x,y,a)=ax-\frac{(1+a^2)gx^2}{2v_0^2}-y$
とし、 $f(x,y,a)=0$ と $\displaystyle \frac{\partial}{\partial a}f(x,y,a)=0$ を連立して解きます。
　 $\displaystyle \frac{\partial}{\partial a}f(x,y,a)=x-\frac{agx^2}{v_0^2}$
なので頑張って $a$ を消去して計算すると、包絡線として $\displaystyle y=\frac{v_0^4-g^2x^2}{2gv_0^2}$ が得られます。